|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Research Results |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
Select from the following findings of the National Assessment of Educational Progress to illustrate some of the common problems in teaching decimals. Each of these three results involve students in the 7th grade (13 years old). You may wish to discuss these results and obtain suggestions from teachers as to why the incorrect answers were selected for the given questions. For further examples see National Assessment of Educational Progress.
|
|
|
|
The first result below is from the second assessment and shows a common misunderstanding involving inequality of decimals. Students tend to select the larger whole number
and in this example
is larger than 2. The Decimal Square for thousandths helps to provide a visual understanding of why .2 is greater than .195
because the square for .2 has 2 full columns shaded whereas the square for .195 has just under 2 full columns (each column has 100 small parts).
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
.195 < .2 |
|
|
|
|
|
 |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
The next result below is from the third assessment and indicates the lack of understanding or rounding and estimating. The NCTM Standards say that students’ use of numbers should be a "sense-making experience" and the results from the following question show that this is often not the case. The percents in the table for the answers to this question are not much better than what might be expected from random guessing.
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
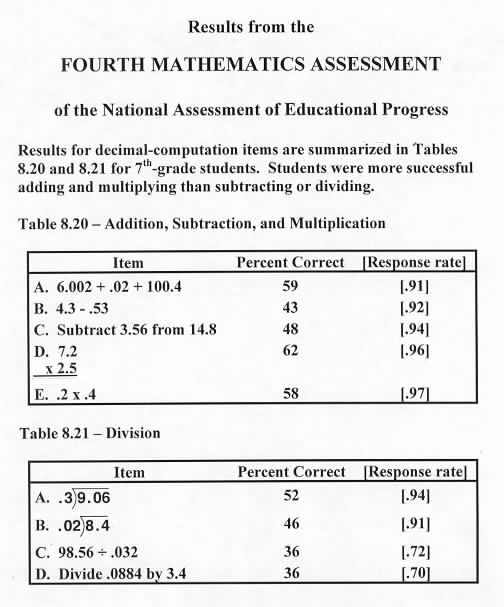
The next result is from the fourth assessment and involves all four basic operations on decimals. Notice that 9% did not respond to the addition exercise in Table 8.20 and 59% gave the correct answer. By modeling the decimal parts of the mixed decimals in this exercise with Decimal Squares
is 2 parts of a thousandths square
is two parts of a hundredths square
and .4 is 4 parts of a tenths square. The sum of these decimals is .422 and the sum of the whole number parts of the mixed decimals is 6 + 100 = 106. So
the sum of the mixed decimals is 106.422. Similarly
the subtraction exercise in Table 8.20 can be visualized using Blank Decimal Squares for hundredths
shading squares for 4.3
and crossing off 53 parts out of 100 to obtain 3.77. Even after students have been taught rules for computing
if they have had visual models that were meaningful
they can often obtain answers through the use of these models.
|
|
|
|
|
|
 |
|
|





